Физическая сущность парадокса близнецов

 

Павло ДАНЫЛЬЧЕНКО

 

Полная версия статьи PDF (190 кб), DOC (51 кб).

P. Danylchenko

Physical essence of twins paradox

It is shown that imaginary twin paradox takes place in special relativity (SR) only because of the impossibility of mutual distinguishing of standard time (path-like proper time of moving object) and coordinate-like proper time of the inertial frame of reference (IFR) and because of neglect of the necessity of re-calculation of time coordinates of events after the transfer of twin-traveler from one IFR to another that moves in reverse direction.

 

 

Реферат

 

 

Хотя мнимому парадоксу близнецов (паралогизму часов) и посвящено множество как научных, так и научно-популярных работ, ни в одной из них до конца так и не вскрыта истинная его физическая сущность. Обычно этот парадокс объясняют тем, что один из близнецов все время движется с постоянной скоростью, а другой, кроме того, в определенные моменты времени совершает еще и ускоренные движения. Такое объяснение указывает лишь на неравнозначность условий движения близнецов. Однако оно все же не разъясняет, почему возраст близнеца-путешественника будет всегда меньше возраста близнеца-домоседа, независимо от длительности их относительного движения с постоянной скоростью а, следовательно, и независимо от величины разницы возрастов, накопившейся в процессе этого равномерного движения в их инерциальных системах отсчета пространственных координат и времени (ИСО). Ведь во всех мысленных экспериментах с идентичными мировыми линиями (МЛ) участков ускоренного движения близнеца-путешественника из-за этого ускоренного движения должна возникать одна и та же конечная разница в возрасте близнецов. Первая же разница, в отличие от этой конечной разницы возрастов, в ИСО каждого из близнецов может достигнуть сколь угодно большего значения. И поэтому, эти разницы все же будут приводить к взаимно противоречивым сведениям о возрасте близнецов. Вскрытие физической сущности мнимого парадокса близнецов и является целью этой статьи.

Первопричины парадокса близнецов.

Специальная теория относительности (СТО) допускает существование особой (выделенной) системы отсчета пространственных координат и времени (СО) – фундаментальной СО неувлекаемого движением физического вакуума (ФВ), в которой частота реликтового излучения изотропна [1]. В евклидовом фоновом пространстве этой сопутствующей Вселенной СОФВ и будем рассматривать движение объектов, однако, не в отсчитываемом в ней космологическом времени, а в пропорциональном ему квантовом собственном времени эталонного вещества, условно покоящегося в этом пространстве. При этом положим, что покоящееся эталонное вещество (ПВ) идентично эталонному веществу движущихся объектов. На рисунке показаны МЛ в СОПВ равномерного движения двух объектов вдоль одной и той же прямой линии. Первый из них, на котором находится близнец-домосед, движется с абсолютной скоростью V₀,, а второй, на котором находится близнец-путешественник, сначала удаляется от первого с относительной скоростью v₁=(V₁–V₀)/(1–V₁V₀), а затем сближается с ним с относительной скоростью v₂=(V₂–V₀)/(1–V₂V₀). Здесь: V₁ и V₂ – абсолютные скорости движения второго объекта соответственно в прямом и в обратном направлениях. При этом принято, что калибровочно инвариантное в квантовом времени эталонного вещества значение постоянной скорости света: c=1.

 

 

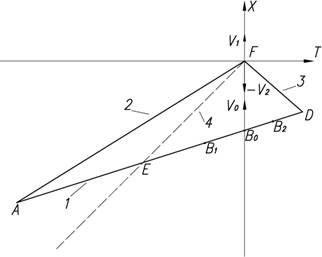
Рис.: 1 – МЛ первого объекта; 2 – МЛ второго объекта во время его удаления от первого объекта; 3 – МЛ второго объекта во время его сближения с первым объектом; 4 – МЛ света.

 

Пусть в СОПВ одновременно с приходом второго объекта в точку F первый объект приходит в точку B₀, а длительность собственного времени движения второго объекта из точки A в точку F равно Δt₁. Тогда соответствующий этому времени промежуток отсчитываемого в СОПВ времени от момента прихода первого объекта в точку B₀, а второго – в точку F, будет равен: t_A= –Γ₁Δt₁, где Γ₁=(1–V₁²)^–1/2. В зависимости от величины в точке F скорости V_i второго объекта промежутки космологического времени между событиями в точке B_i на первом и в точке F на втором объектах, являющимися одновременными (Δt=0) в ИСО второго объекта, будут равны: δt_i=Γ_iV_i·x_Bi, где: x_Bi – наблюдаемая в ИСО второго объекта координата положения первого объекта. Таким образом, при разных значениях в точке F скорости второго объекта одновременными событию в точке F его СО будут события, соответствующие не одному и тому же положению X_Bi=Γ_i·x_Bi в СО первого объекта.

 

Пусть модули относительных скоростей движения объектов в процессе их удаления и сближения равны друг другу (v₂=–v₁). Тогда в момент изменения направления движения вторым объектом изменение положения первого объекта близнецом-путешественником наблюдаться не будет (x_B2=x_B1). Однако, при этом произойдет переход от одновременности в СО близнеца-путешественника с моментом изменения его движения одних событий к одновременности других событий на первом объекте, соответствующих уже другому положению в СОПВ последнего: X_B2=X_B1(1–v₁V₀)/(1+v₁V₀). То есть, при переходе второго объекта от движения со скоростью V₁ к движению со скоростью V₂ происходит замена положений первого объекта, считающихся одновременными с положением второго объекта в точке F. Тем самым, как бы возникает наблюдаемый в СО близнеца-путешественника перепад координатного времени, соответствующего событиям на первом объекте. И, следовательно, имеет место исключение из рассмотрения части путиподобного (стандартного [2]) собственного времени первого объекта, определяющего возраст близнеца-домоседа. Поэтому-то и возникает у близнеца-путешественника ложное умозаключение об уменьшении суммарного времени, истекшего на первом объекте с момента разлуки до момента его встречи с находящимся на этом объекте близнецом-домоседом. Это и является физической сущностью мнимого парадокса близнецов.

 

Результаты непосредственных наблюдений

С учетом перепада координатного времени полное стандартное  (путиподобное собственное) время первого объекта, наблюдаемое близнецом-путешественником, будет таким же как и в СО первого объекта. Наличие перепада собственного времени первого объекта («наблюдаемого» близнецом-путешественником опосредствованно через две его ИСО) отнюдь не означает, что информация о событиях, произошедших на первом объекте между точками B₁ и B₂, не поступает на второй объект. В момент изменения направления движения второго объекта к нему поступает информация о событии, произошедшем на первом объекте в тот момент времени, когда он находился в точке E.

 

Сразу же после изменения направления движения второго объекта изменится и наблюдаемое близнецом-путешественником смещение спектра излучения первого объекта. Это может привести к ложному заключению этим близнецом, что первый объект удалялся от него лишь в течение меньшего времени, чем на самом деле, и уже приближается к нему в течение некоторого времени. И, следовательно, промежутки собственного времени первого объекта, соответствующие взаимному сближению и удалению объектов, будут рассматриваться близнецом-путешественником как имеющие иные значения, нежели наблюдаемые в СО первого объекта близнецом-домоседом. Однако это несоответствие вполне объяснимо неверностью определения (сделанного из ложной предпосылки об изменении направления движения не вторым, а первым объектом) близнецом-путешественником момента прекращения удаления и начала сближения объектов по часам первого объекта. Несмотря на это суммарное значение собственного времени первого объекта, наблюдаемое близнецом-путешественником, будет таким же каким оно наблюдается и в СО первого объекта близнецом-домоседом. А это значит, что на второй объект поступает информация обо всех событиях, произошедших на первом объекте. Из-за движения второго объекта в прямом и в обратном направлениях с разными абсолютными скоростями сокращение расстояний между объектами до и после изменения его движения будут наблюдаться близнецом-путешественником неодинаковыми. При этом изменение расстояния до точки E вследствие неодинакового релятивистского сокращения размеров может привести к взаимному псевдоналожению мнимых промежутков времени взаимного сближения и удаления объектов по часам близнеца-путешественника, отсчитывающим стандартное (путиподобное) время. Это взаимное псевдоналожение промежутков времени обусловлено удалением первого объекта из положения с координатой x_E1 в положение с координатой x_E2 со скоростью большей скорости света в точке наблюдения. И как бы плавно не происходил переход от V₁ к V₂, при таком "наблюдении" (опосредствовано через две ИСО) будет иметь место как бы "течение времени вспять", связанное с переходом второго объекта и находящегося на нем близнеца-путешественника из одной ИСО в другую. Непосредственное же наблюдение, как было показано ранее, этого не обнаруживает. Данный псевдоэффект связан с расчетом значений промежутков времени взаимного сближения и удаления объектов, исходя из предположения об одинаковости несобственных (координатных [3]) значений скорости света (v_c=1) во всем собственном пространстве второго объекта, движущегося не инерциально в процессе перехода от равномерного движения со скоростью V₁ к равномерному движению со скоростью V₂. На самом же деле, это предположение ложно. Несобственные значения скорости света в точках нахождения первого объекта в процессе его перемещения с расстояния x_E1 на расстояние x_E2 не могут быть меньше скоростей перемещения первого объекта в СО второго объекта. А ведь эти скорости значительно превышают скорость света в точке наблюдения смещения спектра излучения, что имеет место из-за чрезвычайно быстрого изменения в СО второго объекта релятивистского сокращения расстояния до первого объекта.

 

При учете изменения несобственного значения скорости света в собственном пространстве второго объекта в процессе его неинерциального движения рассмотренное здесь наложение времен в СО второго объекта наблюдаться не будет. Стандартное время, определенное в этой СО по количеству цугов волн, пришедших от источника стандартного излучения первого объекта, будет совпадать с его значением, определяемым по покоящимся на первом объекте часам.

 

Заключение

Физическая сущность мнимого парадокса близнецов (паралогизма часов) заключается в игнорировании необходимости перерасчета временных координат событий при переходе из одной ИСО в другую. Во избежание подобных паралогизмов необходимо также учитывать, что несобственные (координатные) значения скорости света [2] в СО ускоренно движущихся объектов могут сколь угодно превышать собственное значение скорости света, являющееся калибровочно неизменной величиной лишь в точке дислокации часов, по которым оно определяется [1].

 

Полная версия статьи PDF (190 кб), DOC (51 кб).

 

Литература

1. П. Даныльченко, в сб. Калибровочно-эволюционная теория Мироздания, 1, Винница (1994), с. 10; в сб. Калибровочно-эволюционная интерпретация специальной теорий относительности, О. Власюк, Винница (2004), с. 17, E-print archives, http://n-t.org/tp/ns/ki.htm; Нова книга, Винница (2008), с. 24, E-print: http://pavlo-danylchenko.narod.ru/docs/Foundations_Rus.html.

2. К. Мёллер, Теория относительности, Атомиздат, Москва (1975).